The Trouble with Naming Notes

A straight-forward lesson on note naming from beginner to pro.

Variations and Rules

When students first get into music they start to learn about the names of notes. While there are only seven letters used: A through G, there are variations and rules. These rules can be confusing at first, but if we understand them in steps then the rules make perfect sense. The problem for many students is that instructors don’t want to bury a novice musician with too much information.

To combat this stigma, I’ll explain why we name notes a certain way in steps. As we understand each rule, we can begin to understand how the names of notes reflect the key signature. This gives us information on how specific notes are related to each other, which makes reading and playing music a logical process. Towards the end we’ll begin to work on collections of notes that break some of the rules. While it may appear to be yet another learning task to tackle, these rule breaks also give us information of what has been added to a scale. So, let’s get started.

Each Letter Appears Once

Most scales that musicians use have seven notes, so using the notes A through G works perfectly. The first thing that tends to trip up beginner students is that the C Major scale uses the notes A through G, but starts on C. This information can easily be seen as a strange way of naming notes. A good way to avoid this confusion is to understand that if you play the notes of C Major, but start on A, then you have the A Natural Minor scale. Don’t think of it as two different scales. Imagine the notes C, D, E, F, G, A, and B all working together to make music. If we allow C to be the central point of our music, then we are using a Major scale sound. If A is the central point, then we are in a Minor scale sound. It’s a lot like two sides of a coin. In this case it’s the sound of major or minor.

So, if notes can be rearranged to make new sounds, then why use letters at all? Note letters can be used a lot like words. The word “apple” can be associated with words like “tree”, “food”, and “red”. In music we can use the note C and associate D with it, we can say that D is the second degree of C because it is a whole step above C. That’s a lot of information: degrees, steps, and notes. But that’s a good thing. Now C and D have a relationship. If we were to sharpen or flatten one of these notes, then that relationship changes. Therefore, “C” and “D” have musical meaning.

Now back to the rule of using each letter only once. Check out the chart below. In it you’ll find that (1) each key starts with its letter, (2) the spacing from one degree to the next is the same in each row, and (3) each letter appears only once in a key. I’ve highlighted the sharp and flat notes so that you can watch them build up as we move away from C Major / A Minor, which has no sharps or flats.

The Order of Sharps and Flats

Now that we have a visual representation of the first rule, we should focus on why those sharp and flat notes build up the way they do. This means learning the Order of Sharps and Flats, which is F, C, G, D, A, E, B forward and backward. Check out the next chart with a few examples.

Above we have the Order of Sharps and below is the Order of Flats. Notice how it’s the same set of letters: F, C, G, D, A, E, B. Sharp notes are added to one key at a time. As we go from one key to the next, we gain an additional sharp note from the Order of Sharps.

So, starting with C Major we have no sharp notes. Next is G Major with only one sharp note, which is only the first note from the ordered list. D Major has two sharp notes, so it gets the first two notes from the ordered list: F and C. This means we can write out the letters D through C and sharpen only F and C to get the notes of D Major: D, E, F#, G, A, B, C#.

The same process is used for the flat notes in flats keys. Starting with C Major we have no flat notes. Next is F Major with just one flat note: Bb. The next key is Bb Major with two flat notes. The two letters at the bottom of the list are B and E, so Bb Major’s notes are Bb, C, D, Eb, F, G, A.

Back to the Circle of Fifths

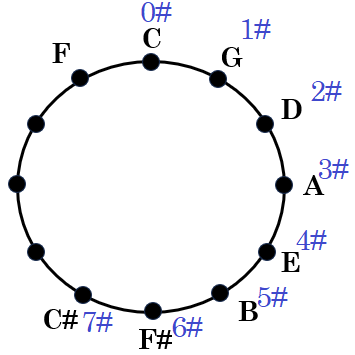
Great! We now have a way of knowing what notes we alter for each key. But how do we know what key to add sharps or flats to? We can use the same Order of Sharps to build the Circle of Fifths. C is at the top of the circle shown below. Look for the Order of Sharps on the circle. Those letters: F, C, G, D, A, E, and B complete half of the circle. We then go two steps farther and start the ordered list over, so F and C are used again but with sharps. The reason for this is because the three keys at the bottom of the circle can be sharp or flat, so we are accounting for the sharps ahead of time. Another reason is because eventually we will have C# Major which has all seven notes with sharps. The number of sharps in a key are notated in blue text.

Now we need to complete the circle with the flat keys. So, we start at the top with C, go left to F, and then write in the Order of Flats as we complete the circle. The Order of Flats is B, E, A, D, G, C, and F, so we write in Bb, Eb, Ab, Db, Gb, and Cb. There is no key of Fb Major because once we reach Cb Major we already have a key with seven flat notes. As you practice writing the letter names of each key around the circle it wouldn’t hurt to include the number of sharps or flats next to it like I’ve done in these two charts.

With all our letter names and the number of sharps and flats accounted for we can use the Order of Sharps and Flats to find the notes in any key. Below we have the completed circle, the order, and the keys of Db Major and E Major. Db Major has four flats, so we write out the letters in alphabetical order starting with D. Then we add the flats to the first four letters in the Order of Flats: B, E, A, and D. The same process happens with E Major, which has four sharps. We write out all the letters once starting with E, then we sharpen the first four letters from the Order of Sharps. This works for all fifteen available keys.

No Key Signatures Necessary

With the Order of Sharps and Flats you can now figure out how many notes are sharp or flat in any key signature along with the structure of the Circle of Fifths. But what happens when another musician shows you a song they are working on? It might only be a few chords like E major, B major, and either F# minor or Gb minor. That’s OK.

With E major and B major we know we are not into the flat side of the circle. If we were, then we would have Eb and Bb. So, we know that our notes are sharp. Using the notes of each chord gives us E-F#-B, B-D#-F#, and F#-A-C#. Putting those notes in alphabetical order gives us A-B-C#-D#-E-F# and an unknown G note.

Using the Order of Sharps, we can look at how far down the list we’ve gone. D# is the lowest sharp from the top of the list, so we know we have a key with at least four sharps. We also know that the notes in the list above D must be sharp as well, so our key must include F#, C#, and G#. G# is our missing note! With the Circle of Fifths in hand we also know that a key with four sharps starts with E. Now we know that the song being shown to us uses E major as the I chord, B major as the V chord, and F# minor as the ii chord.

Being able to logically figure out sharps, flats, and keys is incredibly useful to any musician. Jazz players can use this knowledge as a road map for all tonalites, while Punk Rockers can figure out what root notes their power chords can be paired with. This also helps with music notation. If you have a key signature with three sharps, then you are in A Major. But suddenly the note G# is played as G for several measures. Since we lost the third sharp note in A Major (F#, C#, G#), we can look to D Major as the temporary key signature.

Keep practicing these techniques in as many different keys as you can. Don’t let yourself get comfortable with just the sharps keys and miss out on the fun of the flat keys. Next week we’ll dive into some advanced note naming and how it can help you figure out what a composer is telling you. Until next time!