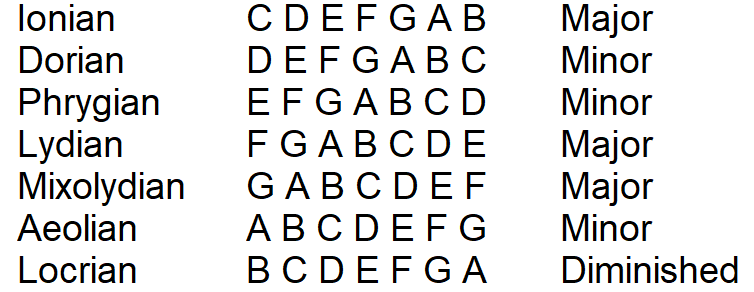Getting Started with the Circle of Fifths

The circle of fifths has so much to offer that people will sell it as charts in books, on posters, on coffee cups and more. Now I'll show you how to write out the entire circle and own it in steps.

A Circular Concept

Before we jump straight into learning the circle of fifths, let me just say this is a concept that I never really appreciated until I started improvising over more than one key. For the longest time I viewed it solely as an academic project. So-what if the notes are all spaced out? They’re just notes, right? Oh, how wrong I was.

I didn’t see the power of this concept until I used it through modulations. It really helps me to understand how the modes sharpen or flatten between keys and which notes change when I modulate between keys. A broader description of this  is that I can play a seven-note scale and by sharpening or flattening one note I can change to a new key. This circular concept helps you to know what note to alter and how to use the new key. These keys provide a new set of sounds that is a lot like speaking as you normally would, but then speaking in a lower pitch. Your words don’t change, but the tone does. The same thing happens when you change keys. Your scales and chords become brighter or deeper depending on how you move around this circular concept. Of course, I first had to learn how to write the circle down from memory, which is easy if you know your modes in fifths and in the key of C. To do this we need to understand what a fifth is.

Defining a Fifth

A fifth is a three and a half step interval or seven half steps. If you start at C and go up to G, then you’ve gone up a fifth in pitch. This interval is named “a fifth” because it takes you to the fifth degree of the major scale. It’s that simple. The C major scale starts on C and the fifth note in that scale is G because it is the fifth degree. The same goes for all the other notes. You could start at C and going up to D is a major second, C to E is a major third, C to  F is a perfect fourth, C to G is a perfect fifth, C to A is a major sixth, and C to B is a major seventh. There are minor intervals for all the degrees except the fourth, but for now let’s focus on the fifth. We will also use the fourth, but we’ll get to that shortly.

Ordering the Modes

The other concept you need to know is the order of the modes. If you don’t know what a mode is, then think of it as starting on a note in the major scale and going through all the notes to come back to where you started. The first mode of the C major scale would start on C and on B. The next mode starts on D and ends on C. Here’s quick list of the modes by name for the C major scale, what notes they use, and if the scale is major, minor, or diminished. Try them out while treating the first note as “home base” or where your melodies resolve to. You’ll notice that each on has a particular flavor.

Memorization Through Recall

At this point you’re probably wondering how to memorize these. I started learning them by first memorizing a phrase, which was “I Don’t Play Loud Music After Lunch.” This way I could just focus on, “I Don’t Play” and “Ionian Dorian Phrygian”. I would repeat that on an instrument playing C major for Ionian, D minor for Dorian, and E minor for Phrygian. After doing that I would walk away from music physically and mentally and come back about thirty minutes to an hour later. Now it was time to recall what I had learned. Using recall is the best way to reinforce what you know so that you don’t forget it. I would then learn “Loud Music After Lunch” and play F major for Lydian, G major for Mixolydian, A minor for Aeolian, and B diminished for Locrian. After doing this process of recall between tasks for about a week I was able to do more than just memorize a silly phrase. I would call out which note in the C major scale and its associated chord for the corresponding mode. I then took a week to play C major scale chords and would call out the mode for every chord that I played. If I was practicing a song, then I was calling any C major chord “Ionian”. After this two-week process, I was able to confidently know what mode I was using in chord form. Then it was time to learn the modes in fifths.

The Modes in Fifths

If you start at the fourth chord you will have your Lydian chord. In the C major scale this is F major. You then go up a fifth from F to C, then C to G, and so on to create this pattern.

This helps in so many ways because now all three major modes are grouped, all three minor modes are grouped, and the one diminished mode is at the end. This pattern also helps because it is the order that we will use to construct the circle of fifths. Before we do, I’d just like to mention that this also can be called the circle of fourths. This is because moving clockwise lets you move up in pitch in fifths while counterclockwise lets you move down in pitch in fifths. The circle of fourths concepts for this exact same circle would have you move clockwise and down in pitch to move in a fourth while moving counterclockwise and up in pitch would also be a fourth. That can be confusing so lets just stick with fifths since we are using the modes in fifths.

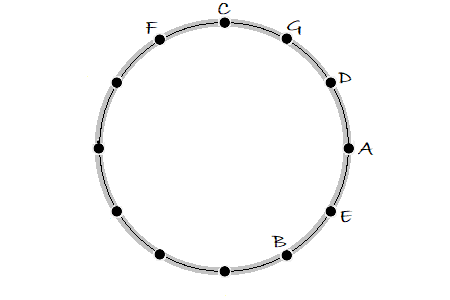
Building the Circle

Below is the circle with just the notes for the C major scale. C is at the top because the key of C has no sharps or flats. There are only natural notes. The other keys will all have sharps or flats, but not sharps and flats. Each of the notes on the circle represents a key, which is like saying where Ionian starts. We’ll cover more on modes in other posts, so to keep things simple let’s stick to our order of the modes in fifths.

Adding the Flats

Now we need to add in the rest of the notes. Start at F and go counterclockwise and backwards through the modes. As we write these next five keys in, we will also flatten them. This means that we start at F Lydian and go clockwise to B Locrian but flatten it for Bb. Next is E Phrygian as we go backwards through the modes, so we write Eb. We follow that with A Aeolian but flatten it for Ab, D Dorian but flatten it for Db, and finish with G Mixolydian for Gb. The final step is to add in the harmonic equivalents of the bottom three keys. A harmonic equivalent is simply the other name for the same note, so G#’s equivalent is Ab.

Listing the Notes

Now that we have our keys in place, we can write in all the notes for fifteen keys. This is not a difficult task once you know how to do it. There are a few steps, so let’s start with the note naming convention. When naming notes in a scale you would use each letter once and only once. The G major scale is G, A, B, C, D, E, F#. The F# could be called Gb but if we did that, we would have two “G” notes. This would be improper and very confusing, especially when we start modulating. Modulation between neighboring keys will share all the same notes except for one. If we can think of our sharps and flats as replacements for the natural note, then we can think of those sharps and flats as modifications to the natural notes. This is like saying A can be modified to either A# or Ab, but once we go in a sharp or flat direction, we must modify any other notes in the same direction. Let’s start naming the notes so you can see what I mean. If you play piano or have access to one even if its on your phone, then this modification idea might make more sense.

The example below has all the notes for each key without any sharps or flats added just yet. Notice how each key starts on its note and only has each letter used once.

Adding the Sharps

Now we will add in all the sharps staring on the right side with G. The way we do this is by keeping all the notes from the previous key, which would be C, and adding the last note as our new sharp to give us F#. The next key is D. We take all the notes from the key of G, including the F#, and add a sharp to the last note to gain C#. The next key is A. Keep C# and F#. Now add G#. That’s all there is to it. This is also a great way to learn note in various keys. You know the key of C because it is all natural notes. By adding F# and starting at G you now have the key of G and the G major scale. In fact, all these keys are what the major scale looks like starting at any note.

Notice that the key of F# has E# as the last note rather than F. Remember that this is due to the naming convention. We already have an F that happens to be sharp, so F natural cannot be used. This means that the last note of E must be sharpened to be the harmonic equivalent of F. The same goes for the key of C#. We already have a C note that again happens to be sharp, so the last note cannot be C and must be B# to be the harmonic equivalent of C.

Adding the Flats

Next, we’ll go counterclockwise from C at the top and add in the flats. The way we do this is very similar to what we did with the sharps. We keep the notes we had before, but now we add the new flatten note to the fourth degree or fourth note in the key. The key of F will start with the same notes in the key of C but will gain a Bb because it is the fourth of the key. This is where the concept of the circle of fourths comes in. Below is that same circle with the flats added in.

Notice how as we move through either side that we can add sharps or flats until we have seven altered notes, which are non-natural notes. The last three sharp keys have equivalent flat keys. This can help you out a lot. Suppose you are in the key of Ab and you go flatter. You would go to Db because all you add is one more flat note. It is much simpler to be in Ab and have a natural G and then move to Db with all the same notes and all you must do is start on Db and add a Gb to your scale. The only other option is to use the key of C# which as seven sharps. This can also be useful because they are the same pitches, and all notes are sharp. You can use whatever you like, but if you modulated back to Ab then staying in flat keys might make more sense.

Adding the Relative Minor Keys

The last thing we’ll add to the circle for this post will be the minor keys. The minor key for any of the major keys is the sixth degree of that major scale, so C major and A minor have the same notes, but C Major starts and resolves to C, while A minor starts and resolves to A. With all the keys listed below, start at C major and C minor. Clockwise for those two positions you’ll get G major and G minor followed by D major and D minor. The pattern for constructing the minor keys is the same as with the major keys. The difference is that you start on the left side of the circle with C minor rather than the top with C Major.

Learn Slowly through Recall and Writing

This is a lot to learn, and you can do it. Just take your time and learn a part or two at a time. You have this post here for you to come back to any time so you can learn how to write this out using the same recall technique that I mentioned earlier. Start with F C G at the top. Then add in D A and when you are ready finished off with E and B. After that you have seven notes down and five to go. Now just go backward for the flats. Take B, E, A, D, and G and flatten them to get Bb, Eb, Ab, Db, and Gb. The next step is to add the harmonic equivalents for the bottom three keys. Now comes the task of naming all the notes, and you know what to do. Write out the letters starting with the keynote. Then add sharps and flats as described above. The part is to notate the minor keys, which is just the sixth note of each matching major key. If you take your time and practice writing this out, you’ll have the whole thing memorized. This took me several weeks to really get it stuck in my head, but now I can pump it out on a dry erase board in a few minutes. What I’m trying to say is that you don’t need to buy any posters or print any fancy internet charts. You can memorize this by taking little steps and using recall.

What this Concept does for You

Now comes the part where everyone asks, “But how do I really use it?” I’ll be writing on this subject in more detail as it applies to a wide variety of topics. Let me give you an example of one of my favorite modulations.

I like to start with the key of C on piano because it uses only the natural notes. Let’s focus on C and use the Ionian Scale: C, D, E, F, G, A, B. As we play this scale, I want to use the note F as an accent in my melodies because soon we’ll go to the key of G and replace that note with F#. To get from the key of C to the key of G I can play the chords Am, Dm, G7, C a few times and then use Am, C, D7, G to get into the key of G. Both keys share Am and C as chords, but the D7 is a dominant chord and is also the fifth of G. This lets me treat G as our new tonic note or note that we resolve to. Now that I’m in this new key, I like to play C Lydian. All that means is that I play the C major scale, but the fourth degree is sharpened, which gives me C, D, E, F#, G, A, B. Just like C Ionian, C Lydian has a C major chord and a C major 7 chord: C, E, G, B. The big difference is that F#. I’ll play that funky note as my new accent in my melodies because it gives me a huge amount of bright tension. I can then use that F# as the seventh of my G Major 7 chord: G, B, D, F#. With that I can do a few rounds of a new progression like Am, C, F#°, GMaj7. (The little circle next to the F# means that chord is diminished.) When I’m ready I can go back to the key of C by playing Am, C, F#°, G7, C, Dm, G7, C. This isn’t going to make the top ten charts, but it is a good example. This last set of eight chords starts in the key of G, but the G7 is the dominant fifth of C. That let’s me land right back on a C major chord and it feels like we are now resolving to C. The Dm, G7, C at the end lets me really focus in on C as my tonic note for a strong resolution.

Try out some of your own modulations where notes or chords are the same in two neighboring keys. I’m sure you’ll be intrigued to try out more ideas outside of a basic seven note scale. If you want to learn more about modulations and what the circle of fifths (or fourths) can do for you, then check back for more posts and feel free to subscribe. I greatly appreciate any support from my fellow musicians.

Thanks for reading!

- Jay McNeill