Chord "Shapes" for Beginners and Intermediate Players
Breaking down the shapes into useful ideas.
What is a “Shape”?
In the world of music a shape is a pattern that your hands can fit to that allows you to play chords and scales more easily. A simpler way to think think of shapes is through a physical pattern that you can touch and see.
When I first started learning music, I was learning to play the guitar and thought of the D major chord as a triangle. Later when I started playing piano I thought of the D major chord as a D minor with a raised third that made it’s own triangle shape.
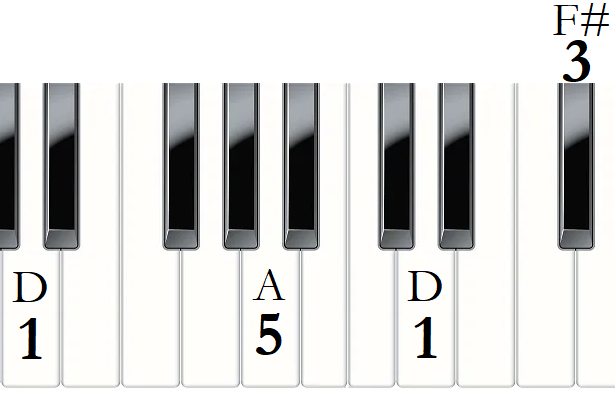
We’ll use D as our tonic for this entire lesson, but before we dive in I’d like to breifly review what we talked about in the last lesson regarding the Major Scale. Below is the D Major Scale. The distance from one note to the next is a half-step. A whole step is therefor two half-steps. In any Major Scale there are only two half-steps: one between degrees 3 and 4, and the other between degrees 7 and 1. All other intervals between degrees is a whole step. This is especially helpful if we want a D major chord that uses degrees 1 3 5. Below you can see that 1 3 5 in the D Major Scale uses the notes D F# A. If we want a D minor chord, then we play 1 b3 5. The only change is the b3 (or flat 3). A flattened F# is just F, so a D minor chord uses the notes D F A.
By knowing where the only two half-steps are we can find degrees 1 throught 7 and then find and flat or sharp degrees as neighbors.
The Main Shape
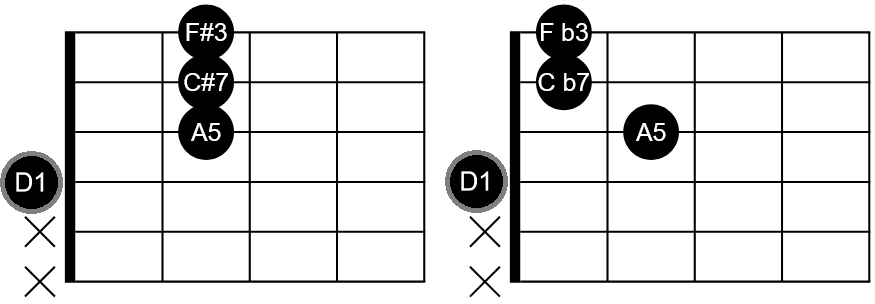
Starting with the D major chord we have the below two shapes for piano and guitar. The piano shape may look odd if you’re new to music, so check out the guitar chart as well. On guitar the lowest notes are to the bottom of the chart and higher pitched notes are to the top. With the guitar’s D major chord arraged as D A D F#, the piano would need to play the same notes in this order with the spacing shown below.
You might be wondering why we need two D notes. Doubling the 1st and 5th degrees is a common result of guitar chord shapes. Doubling the 3rd degree is possible, but can cause issues. If you’re not used to “doubled thirds”, then think of it as an issue that can cause problems or be the answer. For more info on this topic check out “The Taboo of Doubled Thirds”.
Formulas Make It Easier Over Time
Now that we have a “shape”, let’s manipulate it with a formula. From here on out we’ll be using guitar charts for the visual shapes they provide, so here’s a map of the degrees of all notes relative to D for the piano. This will make more sense as we use formulas.
Staring with D major which uses degrees 1 3 5 and D minor which uses degrees 1 b3 5, we can compare the two shapes and see that the third degree is what makes a major or minor chord. I am purposefully not labeling the chords so that you can take your time to compare. Remember: a major uses degree 3 and a minor uses degree b3.
Now let’s focus on the power of shapes. Below is an E major and E minor chord. Notice how we retain the same shape and degrees, but the notes change. On piano the shape can change depending on which key/scale your are in, but fear not. If the key/scale you are using contains a D major chord, then that shape will be present in the key/scale you are working with.
Tetra is Just a Fancy Word for Four
Another common practice in music is to use four note chords called Tetrachords. The three note chords we used so far, called Triads, only use odd degrees by skipping every other note. Tetrachords are no different. A D△7 (or D major 7) and Dm7 (or D minor 7) use a seventh degree. In the D△7 chord we use only natural degree so there are no flats. D△7’s degrees are 1 3 5 7. Dm7 uses a b3 and b7 with the formula 1 b3 5 b7. To make this happen in the charts below all we need to do is take the higher D note and lower it to the appropriate 7th degree.
As long as the note D is in the base we can continue to manipulate the other notes to fit other formulas. Let’s check out a few more.
Suspensions Negate the Third
The chords Dsus2 and Dsus4 take the 3rd degree and move it down to the 2nd degree or up to the 4th degree. That’s it. Keep in mind that if you see a Dsus chord, then it is a Dsus4 because “sus” means suspend, which in turn means to raise. Any sus2 that you see must have the number 2 in the chord’s name. When we sus or suspend to the 2nd degree we hang the third down to the second. Technical stuff, but it’s good to know.
Since we don’t have a defined third in a sus2 or sus4 we can use these chords as long as they fit the scale. There are ways to use sus2 and sus4 chords even if the notes don’t fit the scale, but that’s for another time.
The Last Few Chords for Today
In the Major Scale, the chord build off of the 7th degree note is a diminished chord. The diminished triad uses degrees 1 b3 b5 and the diminished tetrachord, which is known as a “half-diminished” chord, uses degrees 1 b3 b5 b7. Don’t think of these chords as minor chords. By using a b3 and b5 we create a diminished structure where the distance from from 1 to b3 is three half-steps and the distance from b3 to b5 is also three half-steps. Below we’ll look at the half-diminished version with degrees 1 b3 b5 b7, but first we need to talk about augmented chords.
When a chord is augmented is means to take a major chord and raise the 5th degree, so the formula is 1 3 #5. Again, this is not a major chord. It is augmented and like the diminished chords, it has a similar feature. The distance from degree 1 to 3 is four half-steps, and the distance from 3 to #5 is also four half-steps. This symmetry in intervals is what gives diminished and augmented chords their unique sound. Just keep in mind that there are no augmented chords in the Major Scale. You’d have to use another parent scale to access augmented structures.
Recap and 4 Challenges for Multiple Skill Levels
By starting with the Major Scale in any key we can find degrees 1 through 7. Any flat or sharp degrees are a half-step down or up and are therefor neighboring notes. In other words, if you can locate the 3rd degree then you can find the b3rd a half-step down.
We also have some chord formulas, which are:
Major 1 3 5
△7 1 3 5 7
Minor 1 b3 5
m7 1 b3 5 b7
Diminished 1 b3 b5
Half-Diminished 1 b3 b5 b7
Augmented 1 3 #5
sus2 1 2 5
sus or sus4 1 4 5
Now for the beginner’s challenge. Pick a note and use that as degree 1. Find degree 3 two whole steps higher. Then find degree 5 a step and a half higher than that. With degrees 1 3 5 we have a major chord. Use the formulas above to alter the major chord into the other chords. Remember, degree 7 is a half-step below degree 1 and degree b7 is a whole step below degree 1.
The intermediate challenge is to pick a Major Scale you are familiar with. For each note in that scale look at what chord formulas work off of that note. For example, in C Major Scale the notes are C D E F G A B. Starting on C with can make a △7 with C E G B. Starting on D we can make a m7 with D F A C. We can also make a Csus2, Csus4, Dsus2, and Dsus4. Continue to find as many chord as you can that use the notes from the scale.
The “intermediate plus” challenge is to use the below modes of the Major Scale, find as many chord forms that fit per mode, and then apply them to any Major Scale. Below are the formulas for each mode. Keep in mind that other chord we haven’t mentioned like the Dominant 7, which uses 1 3 5 b7, are fair game. You can even combine ideas and find modes that match a Dominant 7 sus4, notated as 7sus4 or 7sus, and uses the degrees 1 4 5 b7.
Lydian 1 2 3 #4 5 6 7
Ionian 1 2 3 4 5 6 7
Mixolydian 1 2 3 4 5 6 b7
Dorian 1 2 b3 4 5 6 b7
Aeolian 1 2 b3 4 5 b6 b7
Phrygian 1 b2 b3 4 5 b6 b7
Locrian 1 b2 b3 4 b5 b6 b7
The advanced challenge is to use any Major Scale along with degree b6 and create a short 8 bar or less tune. Essentially the b6 creates an overlap between the Major and Harmonic Major Scales. Use either a b6 or a 6 for melodies so that you only have seven notes at a time. The exception is to use b6 as a passing tone in a line like 5-b6-6 or 6-b6-5. Use the previous three challenges to explorer chords and modes within two parent scales.
I hope this process of adjusting chord shapes and using formulas help you to unlock more musical knowledge. Keep experimenting with shapes and you’ll find other patterns slowly but surely.