A Quick Re-Cap
Last week we worked on where note names come from based on the Major Scale they belong to. We also used the Order of Sharps and Flats as a tool that allows us to figure out what notes in a key are sharp or flat. The same order of notes is even tied to the Circle of Fifths. Having a way to use seven letters of the alphabet to figure out and write down any Major Scale notes is incredibly handy.
This week we’ll focus on chord names. There are many chords that can come from multiple scales, but those scales are all neighbors on the Circle of Fifths. As the chord names become incredibly complex, you’ll find that the number of scales that match the chord will decrease. So, let’s jump into it.
Chords with Alternating Thirds
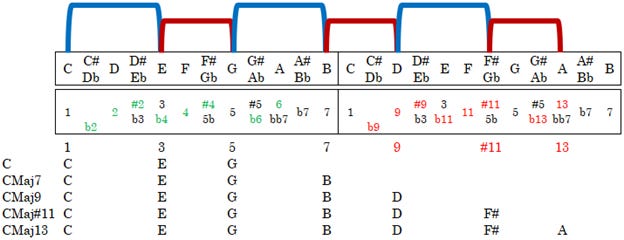
Above we have a visual representation of “alternating thirds”. Working from the middle row and outward we start with the degrees of the Chromatic Scale. These are all the numbered degrees from the Tonic note, shown as 1, and through two octaves. There are some resources out there that treat the second 1 as an 8 to denote that it is an octave above the actual tonic. I like to refer to this as another 1 because the function of that note does not change. Notice how some numbers are green and others are red. The green numbers are the even degrees of the first octave. In the second octave we add 7 to each number to get 9, 11, and 13. This happens because the function of those notes will change between these two octaves.
Above and below are the notes of the Chromatic Scale starting with C. Beyond those rows are blue and red brackets. The blue brackets represent an interval known as the Major Third or “M3”, while the red brackets represent the Minor Third or “m3”.
The way alternating thirds works is we start with an M3 or m3 interval followed by the opposite interval. We continue to “stack” alternating thirds to build our most basic chords. Because of this, you may find this system of alternating thirds referred to as “stacked thirds”. Either approach is fine as we’ll get into the finer details in a moment.
The reason why alternating thirds creates our basic chords is because it creates the least tension. By undulating between M3 and m3 intervals our ears can clearly hear the structure of a chord. If we only used M3 intervals, then we would have an Augmented chord. Using only m3 intervals creates a fully diminished chord. Both chords have high tension because our ears perceive one type of interval. Without a change between intervals our ears have a hard time perceiving the starting point. Alternating thirds can solve this and remove tension by never having one type of “third” next to the same type.
Looking at the above chart we can start at the very top with a M3 between C and E and a m3 from E to G. C is the tonic, E is the Major Third, and G is the Perfect Fifth. A chord played as C-E-G is a C Major chord notated simply as C. If we continue stacking alternating thirds, then the next note is B as the Major Seventh. A chord played as C-E-G-B is notated as CMaj7 because it is literally a C chord extended to the Major Seventh. Adding D to this makes CMaj9 with C-E-G-B-D. Again, this is a C Major chord extended to the Major Ninth. Next up is CMaj#11 as C-E-G-B-D-F# followed by the CMaj13 as C-E-G-B-D-F#-A. Notice how the naming of each chord starts with the three-note triad C-E-G and then assumes every alternating position up to the number in the chord. Below is a chart of each chord mentioned so far.
Starting with a m3 interval gives us another set of chords that all use alternating thirds. Check out the next chart to see the same concept building chords starting with a minor triad.
There are two things to point out with minor chords. The Cm7 chord uses the b7 degree and not the Maj7. If a minor triad used the Maj7 degree, then it would be notated as CmMaj7 and played as C-Eb-G-B. So, any “7” refers to the b7, while Maj7 is specifically Maj7. Now to be thorough, the Maj7 can be notated as a triangle, so you may see CMaj7 and CmMaj7 as C∆ and Cm∆.
The other thing to focus on is that all major and minor chord mentioned so far use degrees 5, 9, and 13. When we combine a M3 with a m3 we get an interval of a Perfect Fifth or P5. So, a blue bracket plus a red bracket is a P5 interval. Starting at the Tonic or 1, we can move through the scale in P5 intervals to always arrive at degrees 5, 9, and 13. Only the thirds, sevenths, and elevenths change.
Non-Alternating Stacked Thirds and Additions
There are plenty of chords that use stacked thirds but break the alternating intervals or omit notes. Above we have the chords C7, Cadd9, and CMaj7(#11). C7 is a C major triad with the b7 degree. This is where knowing that “7” and “Maj7” mean two different degrees.
Next is Cadd9. We start with a C major triad, but then we stop stacking thirds. To get the note D added we literally add it on as degree 9. So, any “add” chord means to take the first part and add one note to it. CMaj7(#11) does just that. It starts with a CMaj7 chord and then adds the #11 note of F#. Remember, if we took a CMaj7 and added the note D, then we would be using alternating thirds, so it is impossible to have a CMaj7add9. That is incorrect and should be named CMaj9 because it extends a C triad to the ninth degree rather than adding it due to a break in stacking thirds.
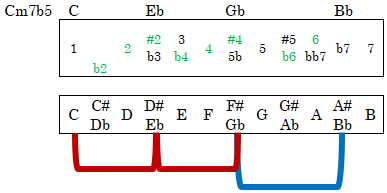
We can also adjust chords. Above is Cm7b5. We started with a Cm7 chord using C-Eb-G-Bb. Then the fifth degree is flattened, so the b5 causes G to become a Gb. The resulting Cm7b5 chord is C-Eb-Gb-Bb.
Implications of Chord Names
Now let’s apply this to some real world concepts. Let’s say you’re jamming with a friend, and they want help making a song more interesting. The song uses the C Major Scale, so our four-note “tetrachords” are CMaj7, Dm7, Em7, FMaj7, G7, Am7, and Bm7b5. The chords they want to improve upon are CMaj7 and FMaj7 with an emphasis on that F-chord.
If you’ve read up on my articles about modes that can be found in the Archives Section, then you’ll be familiar with the fourth mode: Lydian. In C Major, the F-chord is our fourth chord and lines up with the Lydian mode. This mode has degrees 1, 2, 3, #4, 5, 6, and 7. That #4 is what we’ll use to make our friend’s song more interesting.
Now our friend can play their lead melody while we play the rhythm. When we get to the F-chord we play FMaj7(#11) as shown above. This chord is a type of “add” chord, but without the word “add” in it. Instead, we use parentheses to convey the added note/degree. Typically, parentheses are used when the starting chord is more than three notes, so seeing “add” should mean that you are adding to a triad and not a tetrachord. Of course this is music, so there are variations to this.
After playing FMaj7(#11), our friend immediately stops and asks what that was because it worked while being very different. After a quick explanation they ask us to play the C-chord as a CMaj7(#11). That’s were things can go wrong.
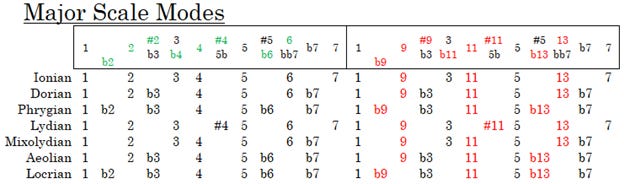
The C Major Scale does not include the note F#, so CMaj7(#11) doesn’t work. In fact, the “Maj(#11)” chords are exclusive to the Lydian mode and other exotic modes that are similar to Lydian. Let’s look at the chart below that uses only degree numbers.
This chart shows the degrees for any Major Scale. Our Friend’s song is in C Major, so the modes start on each note of that scale to create C Ionian, D Dorian, E Phrygian, F Lydian, G Mixolydian, A Aeolian, and B Locrian. These seven modes all use the notes C, D, E, F, G, A, and B.
By using CMaj7(#11), we know that C starts the Lydian mode because the only mode in the above chart that has a “#11” is Lydian. Counting through our letters backwards we can start at C Lydian, move up the list to B Phrygian, continue up to A Dorian, and then arrive at G Ionian. This means that C Lydian belongs to the G Major Scale with the notes G, A, B, C, D, E, and F#.
Notice how the only difference between C Major and G Major are the notes F and F#, yet with the chart of degrees shown above we can see how starting on C Ionian or G Ionian causes a cascading effect. If we played CMaj7(#11) to and from FMaj7(#11) we’d constantly change keys. If the rest of their song really does modulate between C Major and G Major, then this might sound cool. If the rest of the song is strictly in one scale, then this will sound strange unless we can put the modulating chords into context.
Modal Chords
If you are unfamiliar with modes, then this might blow your mind. Below is the C Major Scale with all its modes to include degrees and lettered notes. I’ve included examples of “modal chords” which fit only one mode, causing the chord to bring out the sound of one specific mode. Look for the combinations of degrees that I used like Em7(b9). This only fits E Phrygian because it uses degrees b2/b9 and 5. Those two degrees alone prevent the chord from matching any other mode. Also look at the way thirds are alternated, stacked, and/or omitted. The chord Fadd9(#11) starts with the alternating M3 and m3 intervals to create an F chord as F-A-C. Then we “add” the 9th with G and tack on another note with B as the #11.
Continue to use concepts like note naming, chord naming, notes as degrees, and degrees of modes in conjunction with each other. This will help you to better understand what composers and fellow musicians are using in their arsenal of musical techniques. Adding those techniques to your skill set will make you a better musician.
If you’ve enjoyed reading this or other articles, then please consider subscribing. Your support of my work is incredibly helpful and literally buys me the time to make thorough lessons for you and the music community. You can also share these works and leave comments. I also like to use the comments section as a platform for Q & A. This way you can ask questions about any topic, get an answer, and others can learn from our interaction. With that said, thank you in advance! Until next time.